# Programming01, PPC

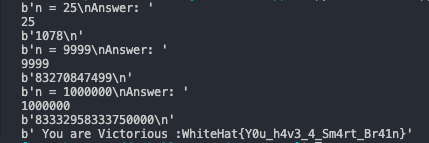
We are given a IP and port to nc to 'nc 15.164.75.32 1999':


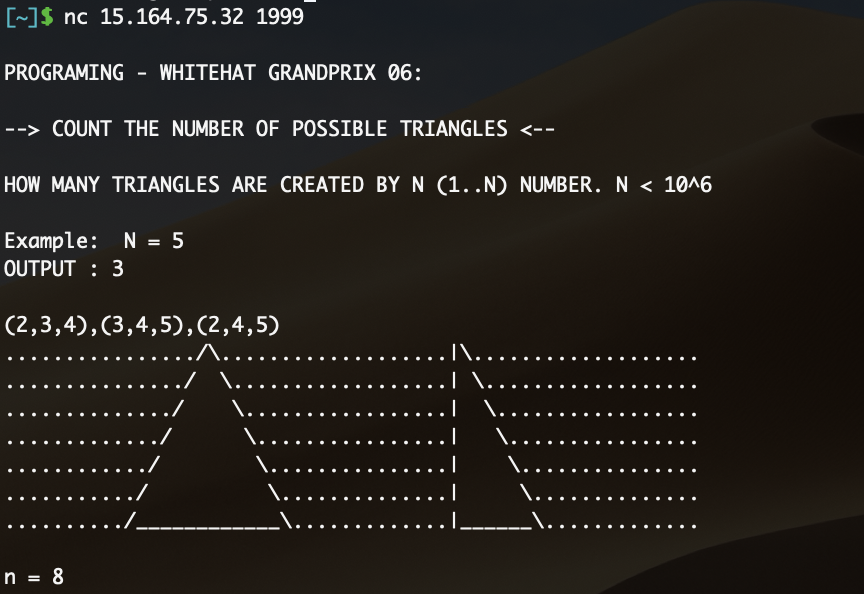
At first, this looks quite confusing. What does the `CREATED BY N` mean? but we can use the example to understand.
The challenge refers to how many triangles and you create with sides length less or equal to n.
So to create a triangle you must follow a + b > c, a + c > b and b + c > a.

We may attempt to brute-force but the challenge specifies N can get as high as `10**6` and brute-forcing is about `O(n**3)` so we must improve the efficiency.
First, let's write all the outputs (for now we're using brute-force) for n 4-14 just to see if we can notice something we can work with.


Now let's see if we can find something in the output, so we'll writing them and let's write the differences also.

```
+1, +2, +4, +6, +9, +12, +16, +20, +25, +30, +36 <---- Differences

0, 1, 3, 7, 13, 22, 34, 50, 70, 95, 125, 161 <---- Outputs
```
You may already notice there are two series here `k**2` and `k(k+1)`.
```
1, 4, 9, 16, 25, 36 <---- k**2

2, 6, 12, 20, 30 <---- k(k+1)
```

So, to know how much triangles there are for a given N we can sum up all the differences up till that N,
so we need the formula for calculating the sum of both of those series.
The `k**2` sum is


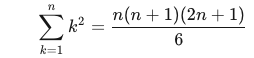
And we can view `k(k+1)` as `k**2 + k` so the sum of `k(k+1)` is


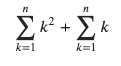
Now all that's left is to know for each N what k are we solving for.
Let's take N=10 for example, there are 50 different triangles and if we look again here
```
+1, +2, +4, +6, +9, +12, +16, +20, +25, +30, +36 <---- Differences

0, 1, 3, 7, 13, 22, 34, 50, 70, 95, 125, 161 <---- Outputs
```
It can be represented as the sum of `n**2` series up to 16 plus the `n(n+1)` series up to 12, so that's `k = 4` and `k = 3`.
If we go up to 11 we will get `k = 4` and `k = 4`.
So we can understand if we're dealing with an even N, k would be `n/2 - 1` for the `n**2` series and `n/2 - 2` for the `n(n+1)` series.
And if it's an odd N, k would be `((n - 1) / 2) - 1` for both.

Now with that information let's implement it all in code:
```python
def n_squared_sum(num):
return int(((num)*(num + 1)*((num * 2) + 1)) / 6)

def n_plus_one_sum(num):
return int(n_squared_sum(num) + ((num * (num+1))/2))

def num_of_triangles(num):
if (num % 2) == 0:
n = (num / 2) - 1
return n_plus_one_sum(n - 1) + n_squared_sum(n)
else:
n = ((num - 1) / 2) - 1
return n_plus_one_sum(n) + n_squared_sum(n)
```

Full code can be found in solver.py


Original writeup (https://github.com/GabiCtrlZ/Whitehat-Quals).