Tags: bitcoin
Rating:
# Scissors Secret Sharing
## Task
A company found a clever way to split its seed used to access their Bitcoin account: it has converted its seed phrase in 12 words with BIP39, and gave one word of the mnemonic to 12 employees.
Alice entered the manager's office and was given the first word on a piece of paper. Then Bob got the second word. Eve entered, and when she opened the door, a draft made all the papers fell on the floor. They are now totally mixed up.
The company is trying to access its funds at address 1EHiMwCPzcvMdeGowsowVF2X2PgLo67Qj7, without success yet. Can you help it?
Flag is CTF{4th word_9th word_11th word_10th word}.
For example, is mnemonic is "satoshi security lonely cupboard magic grow cup buddy cancel desert jar face", address and flag will be: 1J5ryMwcUmb7XiuDPqYjxSywJNf37FNdmA and CTF{cupboard_cancel_jar_desert}.
File: mnemonic.txt
## Solution
Inside the file we have the remaining ten words and the first two words:
```
Alice since
Bob desk
??? zone
??? leaf
??? luggage
??? hobby
??? depart
??? thrive
??? practice
??? carbon
??? prison
??? ivory
Bitcoin address: 1EHiMwCPzcvMdeGowsowVF2X2PgLo67Qj7
```
We now need to write a function that bruteforces all possible permutations of the shuffled words. We can calculate the amount as:
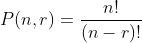
With `n` as the amount of objects and `r` as the amount of spaces. Since `n = r` we can simplify that as `n!`. Which is `3628800` permutations for 10 words.
So, how is BIP39 calculated? We can read that here: https://github.com/bitcoin/bips/blob/master/bip-0039.mediawiki
1. `The mnemonic must encode entropy in a multiple of 32 bits. With more entropy security is improved but the sentence length increases. We refer to the initial entropy length as ENT. The allowed size of ENT is 128-256 bits.`
2. `First, an initial entropy of ENT bits is generated. A checksum is generated by taking the first ENT / 32 bits of its SHA256 hash. This checksum is appended to the end of the initial entropy. Next, these concatenated bits are split into groups of 11 bits, each encoding a number from 0-2047, serving as an index into a wordlist. Finally, we convert these numbers into words and use the joined words as a mnemonic sentence.`
3. `To create a binary seed from the mnemonic, we use the PBKDF2 function with a mnemonic sentence (in UTF-8 NFKD) used as the password and the string "mnemonic" + passphrase (again in UTF-8 NFKD) used as the salt. The iteration count is set to 2048 and HMAC-SHA512 is used as the pseudo-random function. The length of the derived key is 512 bits (= 64 bytes).`
4. `This seed can be later used to generate deterministic wallets using BIP-0032 or similar methods.`
`10!` iterations of `PBKDF2-HMAC-SHA512` with 2048 iterations would take ~6 hours on my machine. We need to get that amount down.
How? See step 2. What that means is: the last word is a checksum. Roughly every 16th permutation has a valid checksum. That's only `226800` permutations.
This answer has a reference for calculating the address from a mnemonic: https://bitcoin.stackexchange.com/a/84548
Now we just need to check if a certain permutation has a valid checksum and then calculate the address to compare it to the one from the task. The `mnemonic` module provides a `check` function:
```python
import mnemonic
import bip32utils
import progressbar
from itertools import permutations
m = mnemonic.Mnemonic('english')
def bip39(mnemonic_words):
seed = m.to_seed(mnemonic_words)
root_key = bip32utils.BIP32Key.fromEntropy(seed)
child_key = root_key.ChildKey(
44 + bip32utils.BIP32_HARDEN
).ChildKey(
0 + bip32utils.BIP32_HARDEN
).ChildKey(
0 + bip32utils.BIP32_HARDEN
).ChildKey(0).ChildKey(0)
return {
'words': mnemonic_words,
'addr': child_key.Address()
}
# Start with the example as sanity check after finding a solution
example = "satoshi security lonely cupboard magic grow cup buddy cancel desert jar face"
out = [{"words":example}]
assert(bip39(example)["addr"] == "1J5ryMwcUmb7XiuDPqYjxSywJNf37FNdmA")
start = ("since", "desk")
shuff = ["zone","leaf","luggage","hobby","depart","thrive","practice","carbon","prison","ivory"]
fac = lambda x: x * fac(x - 1) if x > 1 else 1
# We store the last position to continue at a certain point and
# to use a nice progressbar
done = 0
last = 2059978
try:
with progressbar.ProgressBar(max_value=fac(10)) as bar:
for x in permutations(shuff):
done += 1
if done < last:
continue
join = ' '.join(start + x)
if m.check(join):
bar.update(done)
res = bip39(join)
if res["addr"] == "1EHiMwCPzcvMdeGowsowVF2X2PgLo67Qj7":
print()
print(done, res)
out.append(res)
except KeyboardInterrupt:
pass
except Exception as e:
print(e)
# CTF{<4th word>_<9th word>_<11th word>_<10th word>}
for x in out:
w = x["words"].split(" ")
print(w)
print("CTF{%s}" % '_'.join([w[3], w[8], w[10], w[9]]))
```
The `2059978` permutation is the correct one. If we run this script:
```bash
$ python solve.py
2059978 {'words': 'since desk thrive carbon zone prison leaf depart hobby practice ivory luggage', 'addr': '1EHiMwCPzcvMdeGowsowVF2X2PgLo67Qj7'}
56% (2061337 of 3628800) |####################################################################### | Elapsed Time: 0:00:00 ETA: 0:00:00^C
['satoshi', 'security', 'lonely', 'cupboard', 'magic', 'grow', 'cup', 'buddy', 'cancel', 'desert', 'jar', 'face']
CTF{cupboard_cancel_jar_desert}
['since', 'desk', 'thrive', 'carbon', 'zone', 'prison', 'leaf', 'depart', 'hobby', 'practice', 'ivory', 'luggage']
CTF{carbon_hobby_ivory_practice}
```