Rating:
> Gerald and Gerald have just learned that Gerald has cracked their previous cypher. Gerald scolds Gerald, saying that he shouldn't have given away the key. Gerald, therefore, decides to create a new cypher, hopefully one that Gerald can't crack.
> Author: MichaelK522
For this challenge we are given a more challenging circuit, along with ciphertext.
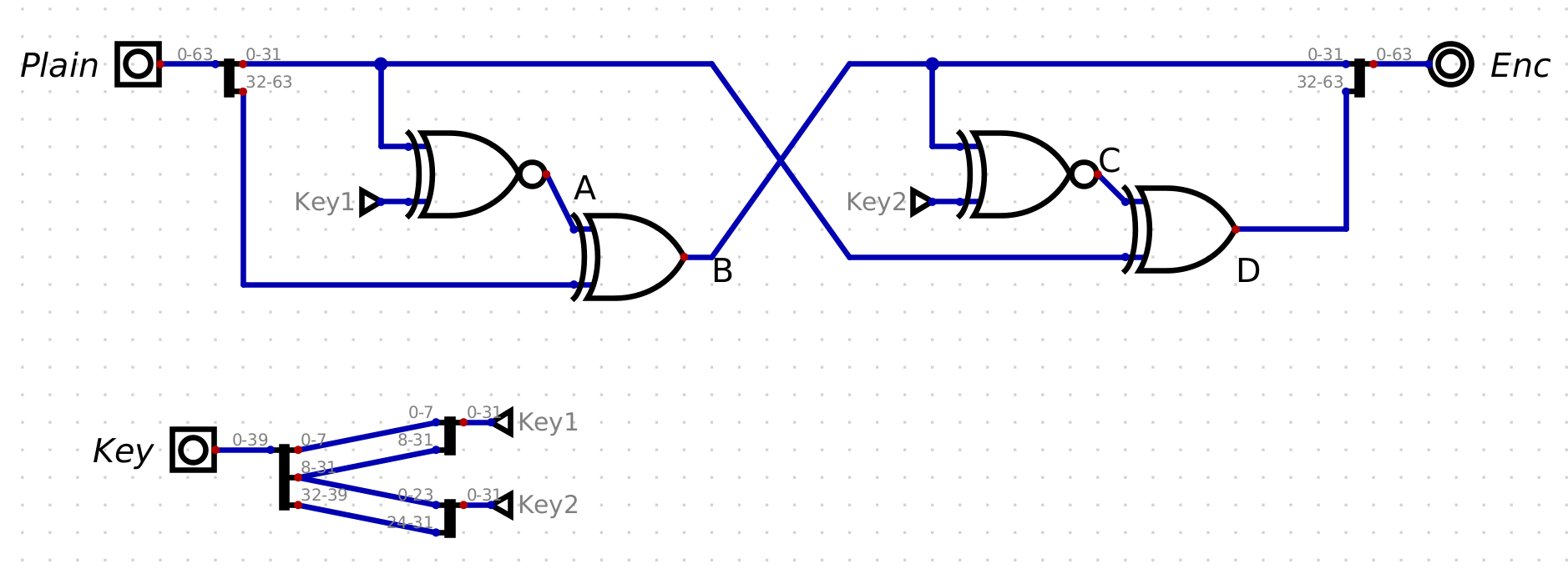
I rewrote the process in python to confirm my understanding
```python
def xnor(a, b): # only need to handle case of 32 bits
return 0xffffffff - (a ^ b)
def encryptor(pt, key):
"""
:param pt: 64 bits
:param key: 40 bits
:return:
"""
print('pt:', hex(pt))
print('key:', hex(key))
ph = pt >> 32 # high DWORD from plaintext QWORD
pl = pt & 2**32-1 # low DWORD from plaintext QWORD
k1 = key & 2**32-1
k2 = (key >> 8) & 2**32-1
A = xnor(k1, pl)
B = A ^ ph # low DWORD from ciphertext QWORD
C = xnor(B, k2)
D = pl ^ C # high DWORD from ciphertext QWORD
output = B | (D << 32)
print('output', hex(output))
return output
```
We know 7 of the first 8 bytes of the flag: `bcactf{`. We can therefore guess the last character to *have* all 8, and then we have enough variables to calculate `key_1`, `key_2` (XNOR is written `v` because I don't know the correct character...):
`B = pl v k1 ^ ph` => `k1 = B ^ ph v pl`
`D = b v k2 ^ pl` => `k2 = D ^ pl v B`
```python
def decryptor():
base_pt = int(binascii.hexlify(b'bcactf{\x00'), 16)
ct = 0x7B18824F93FB072A # first eight bytes from ciphertext
B = ct & 0xffffffff
D = ct >> 32
for i in range(0x20, 0x80): # brute force last char
print('trying i =', hex(i), chr(i))
pt = base_pt + i
ph = pt >> 32
pl = pt & 2**32-1
k1 = xnor(B ^ ph, pl)
k2 = xnor(D ^ pl, B)
key = k1 | (k2 << 8)
if (k1 >> 8 == k2 & 2**23-1):
print('k1', hex(k1))
print('k2', hex(k2))
print('key', hex(key))
print('pt', hex(pt))
```
`k1` and `k2` overlapped, so that could be used to verify the decode was correct. The correct values ended up being:
```
k1 = 0x7a01e2ce
k2 = 0x637a01e2
```
with the last value of the plaintext being `x`. From there we can decode the rest of the ciphertext
```python
def decrypt_now_that_we_know_the_key(ct):
"""
:param ct: 64 bits
"""
k1 = 0x7a01e2ce
k2 = 0x637a01e2
B = ct & 0xffffffff # 2850399423
D = ct >> 32 # 37502721
pl = xnor(B, k2) ^ D
ph = xnor(k1, pl) ^ B
pt = pl | (ph << 32)
return binascii.unhexlify(hex(pt)[2:])
if __name__ == '__main__':
ct = [0x7B18824F93FB072A, 0x2909D67381E26C31, 0x57238C7EFEF9132D, 0x7D24AD42B991216A, 0x464B9173A2811D13]
print('Flag:', b''.join([decrypt_now_that_we_know_the_key(part) for part in ct]).decode())
```
Flag: `bcactf{x0r5_4nD_NXoR5_aNd_NnX0r5_0r_xOr}`