Rating:
# Strike Back
The description for this challenge is as follows:
*A fleet of steam blimps waits the final signal from their commander in order to attack gogglestown kingdom. A recent cyber attack had us thinking if the enemy managed to discover our plans and prepare a counter-attack. Will the fleet get ambused???*
The challenge was rated at 2 out of 4 stars, and it was worth 350 points at the end with a total of 40 solves. The downloadables for the challenge included a .pcap file and a Mini DuMP file. This challenge was reasonably straightforward once you found the correct writeups/scripts.
**TL;DR Solution:** Extract the freesteam.exe file from the pcap and recognize it as part of a cobalt strike attack. Do some research on MiniDuMP files in relation to Cobalt Strike to determine that they can be used to decrypt the beacon's traffic. Use the appropriate scripts to derive keys from the MiniDuMP and apply them to pcap in order to extract the pdf file that contains the flag.
## Original Writeup Link
This writeup is also available on my GitHub! View it there via this link: https://github.com/knittingirl/CTF-Writeups/tree/main/forensic_challs/HTB_Uni_Quals_21/strike_back
## Gathering Information
The more straightforward component is the pcap file, so we can start there. When I open it up in Wireshark, packets 4 and 10 indicate that the file freesteam.exe was downloaded to the victim device over HTTP. File > Export Objects > HTTP gives me a window that I can use to easily extract this file for further analysis.
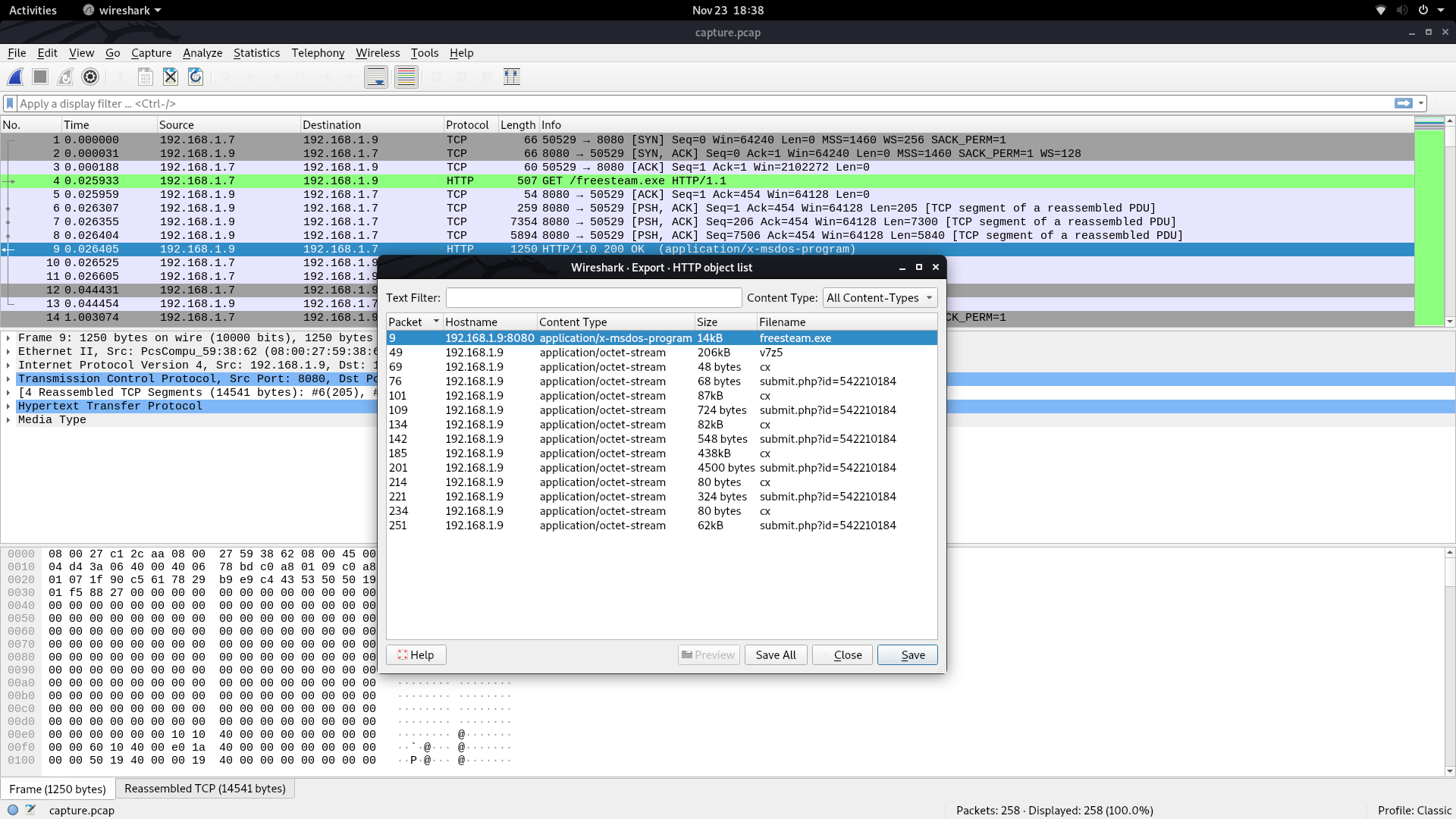
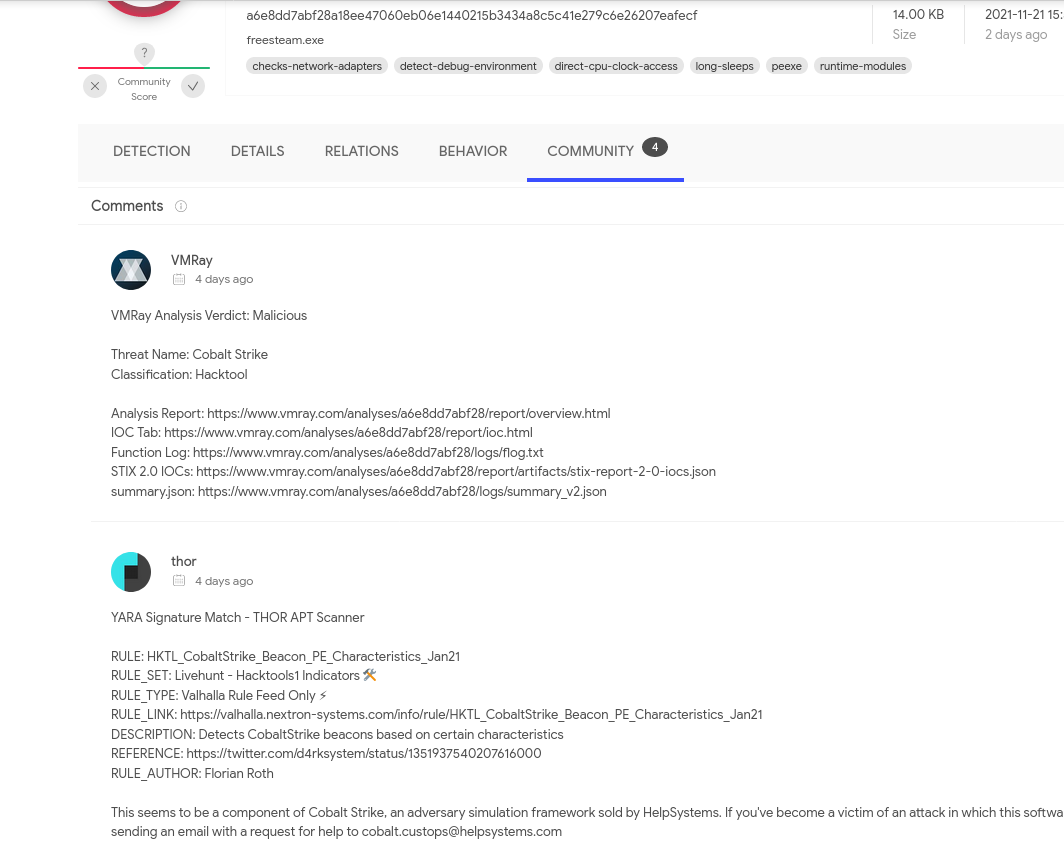
If I upload the file to VirusTotal online, it is very clearly malware, and the Community tab indicates that it is a component of Cobalt Strike.
There is more HTTP traffic in the pcap, but it seems to be encrypted somehow, so it's time to move on to the .dmp file. If I use the file command, I can see that this is a MiniDuMP crash report.
```
knittingirl@piglet:~/CTF/HTB_Uni_Quals_21/forensics_strike_back$ file freesteam.dmp
freesteam.dmp: Mini DuMP crash report, 17 streams, Thu Nov 11 11:40:40 2021, 0x469925 type
```
By using radare2, I can determine that this is a dump for a process of freesteam.exe, which is the Cobalt Strike component from the pcap.
```
knittingirl@piglet:~/CTF/HTB_Uni_Quals_21/forensics_strike_back$ r2 freesteam.dmp
[WARN] Invalid or unsupported enumeration encountered 21
[WARN] Invalid or unsupported enumeration encountered 22
[INFO] Parsing data sections for large dumps can take time, please be patient (but if strings ain't your thing try with -z)!
[0x02dd0000]> iSq~exe
0x400000 0x409000 ---- C:\Users\npatrick\Downloads\freesteam.exe
0x400000 0x409000 ---- C:\Users\npatrick\Downloads\freesteam.exe
[0x02dd0000]>
```
By searching for variations on "Cobalt Strike memory dump", I can see that it should be possible to derive a decryption key for the traffic from freesteam.dmp, then apply that key to the pcap file.
## Decrypting the Traffic
I learned that key extraction from a dump varies based on the version of the cobalt strike beacon. In version three, keys are preceded by a set string of metadata and, false positives aside, can be extracted fairly easily. This approach did not work in this case, so I assume that this sample is from version 4. In this case, you provide the encrypted callback, and a script by security researcher Didier Stevens can be used to test all possible keys in the dump against that callback. Once it is successful, it will print the keys, and you can then decrypt the traffic. This blogpost by Stevens himself describes the methodology: https://blog.didierstevens.com/2021/04/26/quickpost-decrypting-cobalt-strike-traffic/.
I got the encrypted callback from packet number 76; it is a POST request to /submit.php?id=542210184. I then used it against the memory dump to extract AES and HMAC keys:
```
knittingirl@piglet:~/CTF/HTB_Uni_Quals_21/forensics_strike_back$ python3 cs-extract-key.py -c 000000402b765d3e7a22f0e9df40a966705ae4be1bdef5756ccb0eea362e3d33d6ee17764b57a875cabea7bb2c139211385341b80e197d05b49a6668696879976f287aba freesteam.dmp
File: freesteam.dmp
Searching for AES and HMAC keys
Searching after sha256\x00 string (0x30a1b)
AES key position: 0x00438501
AES Key: 5c357fa00554fa9a4928f14795811e40
HMAC key position: 0x0043b821
HMAC Key: 09a36cf8781707756498d7f498211d47
SHA256 raw key: 09a36cf8781707756498d7f498211d47:5c357fa00554fa9a4928f14795811e40
Searching for raw key
Searching after sha256\x00 string (0x431fc9)
AES key position: 0x00438501
AES Key: 5c357fa00554fa9a4928f14795811e40
HMAC key position: 0x0043b821
HMAC Key: 09a36cf8781707756498d7f498211d47
Searching for raw key
```
To decrypt the actual packet capture, I have to use both the HMAC and AES keys with another Didier Stevens script to get the following results, edited down for clarity:
```
knittingirl@piglet:~/CTF/HTB_Uni_Quals_21/forensics_strike_back$ python3 cs-parse-http-traffic.py -k 09a36cf8781707756498d7f498211d47:5c357fa00554fa9a4928f14795811e40 capture.pcap
Packet number: 9
HTTP response (for request 4 GET)
Length raw data: 14336
HMAC signature invalid
Packet number: 49
HTTP response (for request 23 GET)
Length raw data: 206418
HMAC signature invalid
Packet number: 69
HTTP response (for request 66 GET)
Length raw data: 48
Timestamp: 1636630530 20211111-113530
Data size: 8
Command: 27 GETUID
Arguments length: 0
Packet number: 76
HTTP request POST
http://192.168.1.9/submit.php?id=542210184
Length raw data: 68
Counter: 2
Callback: 16 BEACON_GETUID
b'WS02\\npatrick (admin)'
...
Packet number: 134
HTTP response (for request 119 GET)
Length raw data: 82528
Timestamp: 1636630652 20211111-113732
Data size: 82501
Command: 44 UNKNOWN
Arguments length: 82432
b'MZARUH\x89\xe5H\x81\xec \x00\x00\x00H\x8d\x1d\xea\xff\xff\xffH\x81\xc3T\x16\x00\x00\xff\xd3H\x89\x
MD5: 18f9b2ca9e8916b1c3246a4355c1b60f
Command: 40 UNKNOWN
Arguments length: 53
Unknown1: 0
Unknown2: 1391256
Pipename: b'\\\\.\\pipe\\f541a074'
Command: b'dump password hashes'
b''
Packet number: 142
HTTP request POST
http://192.168.1.9/submit.php?id=542210184
Length raw data: 548
Counter: 4
Callback: 21 BEACON_OUTPUT_HASHES
b'Administrator:500:aad3b435b51404eeaad3b435b51404ee:31d6cfe0d16ae931b73c59d7e0c089c0:::\nDefaultAccount:503:aad3b435b51404eeaad3b435b51404ee:31d6cfe0d16ae931b73c59d7e0c089c0:::\nGuest:501:aad3b435b51404eeaad3b435b51404ee:31d6cfe0d16ae931b73c59d7e0c089c0:::\nJohn Doe:1001:aad3b435b51404eeaad3b435b51404ee:37fbc1731f66ad4e524160a732410f9d:::\nnpatrick:1002:aad3b435b51404eeaad3b435b51404ee:3c7c8387d364a9c973dc51a235a1d0c8:::\nWDAGUtilityAccount:504:aad3b435b51404eeaad3b435b51404ee:c81c8295ec4bfa3c9b90dcd6c64727e2:::\n'
...
Packet number: 221
HTTP request POST
http://192.168.1.9/submit.php?id=542210184
Length raw data: 324
Counter: 6
Callback: 22 TODO
b'\xff\xff\xff\xfe'
----------------------------------------------------------------------------------------------------
C:\Users\npatrick\Desktop\*
D 0 11/11/2021 03:26:59 .
D 0 11/11/2021 03:26:59 ..
F 5175 11/11/2021 03:24:13 cheap_spare_parts_for_old_blimps.docx
F 282 11/10/2021 07:02:24 desktop.ini
F 24704 11/11/2021 03:22:16 gogglestown_citizens_osint.xlsx
F 62409 11/11/2021 03:20:47 orders.pdf
----------------------------------------------------------------------------------------------------
Packet number: 234
HTTP response (for request 231 GET)
Length raw data: 80
Timestamp: 1636630835 20211111-114035
Data size: 44
Command: 11 DOWNLOAD
Arguments length: 36
b'C:\\Users\\npatrick\\Desktop\\orders.pdf'
MD5: b25952a4fd6a97bac3ccc8f2c01b906b
Packet number: 251
HTTP request POST
http://192.168.1.9/submit.php?id=542210184
Length raw data: 62588
Counter: 7
Callback: 2 DOWNLOAD_START
parameter1: 0
length: 62409
filenameDownload: C:\Users\npatrick\Desktop\orders.pdf
Counter: 8
Callback: 8 DOWNLOAD_WRITE
Length: 62409
MD5: 938592c96d1cabb8337c37ab71645b24
Counter: 9
Callback: 9 DOWNLOAD_COMPLETE
b'\x00\x00\x00\x00'
Commands summary:
11 DOWNLOAD: 1
27 GETUID: 1
40 UNKNOWN: 3
44 UNKNOWN: 2
53 LIST_FILES: 1
89 UNKNOWN: 1
Callbacks summary:
2 DOWNLOAD_START: 1
8 DOWNLOAD_WRITE: 1
9 DOWNLOAD_COMPLETE: 1
16 BEACON_GETUID: 1
21 BEACON_OUTPUT_HASHES: 1
22 TODO: 1
24 BEACON_OUTPUT_NET: 1
32 UNKNOWN: 1
```
I spent a bit of time with the hashes and found nothing useful, so I moved on to trying to extract the pdf that seems to have downloaded over this encrypted connection. It took me a bit to finally run the decryption script with "--help" and realize that a -e switch was available to extract files to disk. With this slightly modified command, it printed off the same results, but it also added several .vir files to my current directory. The file command revealed that I had several DLL files, an ASCII text file, and one pdf.
```
knittingirl@piglet:~/CTF/HTB_Uni_Quals_21/forensics_strike_back$ python3 cs-parse-http-traffic.py -k 09a36cf8781707756498d7f498211d47:5c357fa00554fa9a4928f14795811e40 capture.pcap -e
...
knittingirl@piglet:~/CTF/HTB_Uni_Quals_21/forensics_strike_back$ ls
capture.pcap payload-18f9b2ca9e8916b1c3246a4355c1b60f.vir
cobalt_virustotal.png payload-2211925feba04566b12e81807ff9c0b4.vir
cs-extract-key.py payload-2cf6d90b7f82a98b03be07b612f2fef3.vir
cs-parse-http-traffic.py payload-938592c96d1cabb8337c37ab71645b24.vir
freesteam.dmp payload-aaef1a752d26993a64e1ede54d93407c.vir
freesteam.exe payload-b25952a4fd6a97bac3ccc8f2c01b906b.vir
freesteam_exe_extraction.png
knittingirl@piglet:~/CTF/HTB_Uni_Quals_21/forensics_strike_back$ file *.vir
payload-18f9b2ca9e8916b1c3246a4355c1b60f.vir: PE32+ executable (DLL) (GUI) x86-64, for MS Windows
payload-2211925feba04566b12e81807ff9c0b4.vir: data
payload-2cf6d90b7f82a98b03be07b612f2fef3.vir: PE32 executable (DLL) (GUI) Intel 80386, for MS Windows
payload-938592c96d1cabb8337c37ab71645b24.vir: PDF document, version 1.4
payload-aaef1a752d26993a64e1ede54d93407c.vir: MS-DOS executable PE32+ executable (DLL) (console) x86-64, for MS Windows
payload-b25952a4fd6a97bac3ccc8f2c01b906b.vir: ASCII text, with no line terminators
```
I renamed the pdf file to orders.pdf and opened it up normally. The flag was in cleartext inside.

Thanks for reading!