Tags: csidh
Rating:
This challenge presents a SageMath implementation of the CSIDH protocol that gives you 600 seconds of interaction in which you can interact upto 500 times but can not send the same public key more than once.
#!/usr/bin/env sage
proof.all(False)
if sys.version_info.major < 3:
print('nope nope nope nope | https://hxp.io/blog/72')
exit(-2)
ls = list(prime_range(3,117))
p = 4 * prod(ls) - 1
base = bytes((int(p).bit_length() + 7) // 8)
R.<t> = GF(p)[]
def montgomery_coefficient(E):
a,b = E.short_weierstrass_model().a_invariants()[-2:]
r, = (t**3 + a*t + b).roots(multiplicities=False)
s = sqrt(3*r**2 + a)
return -3 * (-1)**is_square(s) * r / s
def csidh(pub, priv):
assert type(pub) == bytes and len(pub) == len(base)
E = EllipticCurve(GF(p), [0, int.from_bytes(pub,'big'), 0, 1, 0])
assert (p+1) * E.random_point() == E(0)
for es in ([max(0,+e) for e in priv], [max(0,-e) for e in priv]):
while any(es):
x = GF(p).random_element()
try: P = E.lift_x(x)
except ValueError: continue
k = prod(l for l,e in zip(ls,es) if e)
P *= (p+1) // k
for i,(l,e) in enumerate(zip(ls,es)):
if not e: continue
k //= l
phi = E.isogeny(k*P)
E,P = phi.codomain(), phi(P)
es[i] -= 1
E = E.quadratic_twist()
return int(montgomery_coefficient(E)).to_bytes(len(base),'big')
################################################################
randrange = __import__('random').SystemRandom().randrange
class CSIDH:
def __init__(self):
self.priv = [randrange(-2,+3) for _ in ls]
self.pub = csidh(base, self.priv)
def public(self): return self.pub
def shared(self, other): return csidh(other, self.priv)
################################################################
alice = CSIDH()
__import__('signal').alarm(600)
from Crypto.Hash import SHA512
secret = ','.join(f'{e:+}' for e in alice.priv)
stream = SHA512.new(secret.encode()).digest()
flag = open('flag.txt','rb').read().strip()
assert len(flag) <= len(stream)
print('flag:', bytes(x^^y for x,y in zip(flag,stream)).hex())
seen = set()
for _ in range(500):
bob = bytes.fromhex(input().strip())
assert bob not in seen; seen.add(bob)
print(alice.shared(bob).hex())
After some analysis of the CSIDH implementation we noticed that it is faulty. Occasionally (with probability $1/l_i$) it will fail to walk an isogeny of degree $l_i$ during its isogeny walk. The secret exponents in this implementation are constrained to $\\{-2, -1, 0, 1, 2\\}$. This means that if the exponent $e_i$ is zero, the implementation can not fail to walk an $l_i$-degree isogeny as there is supposed to be no walk, if $\lvert e_i \rvert = 1$ there is one chance for it to fail, if $\lvert e_i \rvert = 2$ there are two chances for it to fail.
We knew that we needed to use these different failure probabilities to get information on the private key which would get us the flag. If we had Alice's public key or could send the same public key more than once we could detect when an error happened, as we could compare the returned shared secret with the expected one. However, we had no clear way to do that. What we thought of next send us on a twisted and long detour where our solution almost worked but not quite. Get it *twist*-ed?
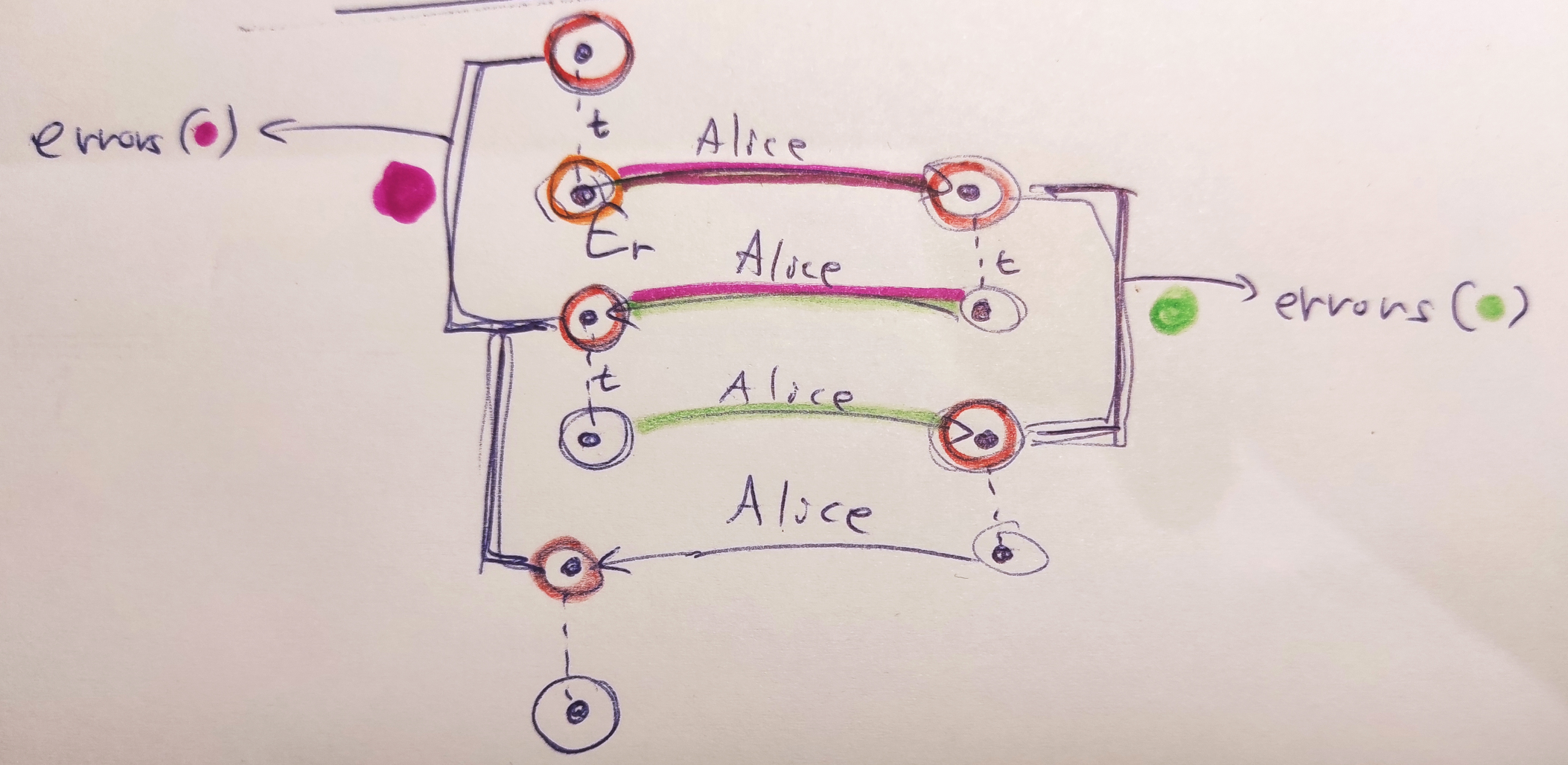
We thought of using twists (shown in the diagram above as $t$) to let Alice walk back and forth between two "neighborhoods" of curves, one neighborhood close to the starting curve (can be $E_0$ or really any curve) and one neighborhood close to her public key. We could then try to find a path between consecutive pairs of curves in each neighborhood using a meet-in-the-middle graph search algorithm. These paths would be the errors that Alice made during her two computations "there" and "back" (on the diagram above the paths are highlighted using colors). We would then aggregate these errors and use their relative frequencies to infer information about Alice's private key.
There were a couple of issues with this approach. First, the $E_0$ curve is special with regards to twists, as twisting it jumps to the second graph component in the isogeny graph (also we thought that SageMath might have some issues computing a twist of this curve correctly). Thinking back at this, it could actually be beneficial to use this fact if the other graph component is somehow smaller to have an easier time searching the neighborhoods. The other issue with this twisted approach is that you can easily only detect errors upto a sign and you will not detect the case when Alice makes the same error during both computations "there" and "back". However, even with these issues our approach almost worked and we spent a good part of a day on looking at its partially good results and trying to figure out where exactly it was going wrong. There was clear signal in the noise as we detected when errors happened in our test runs, but after aggregating the errors we were not getting what we expected.
The idea to ditch the twists came on the last day of the CTF. We finally thought of the simpler solution to creating our two neighborhoods of curves by giving Alice the curve $E_0$, then $[3]E_0$, $[5]E_0$, and so on, obtaining curves $A_0$, $A_1$, $A_2$ then doing $[3^{-1}]A_1$ and so on to map the curves back to the neighborhood. What we got by mapping the curves back were essentially Alice's public key with errors introduced by the faulty algorithm. We counted the unique curves in this mapped set and given that the probability of no error occuring at all during the computation of the faulty algorithm was quite high we could see that the curve that occured the most often was Alice's true public key, without any errors. We could then run a meet-in-the-middle algorithm to find paths between this public key and other mapped curves, these paths were the errors that Alice made during the computation. Compared to the twist approach, here we were getting all the errors correctly and even with the sign intact, as we were searching for paths between an error-less public key and a public key with errors (a single run of the faulty algorithm was involved, not two).
We then aggregated the errors (which matched the private key exactly on smaller instance test runs we did) but then no flag. We weren't sure what had happened and tried to fix errors by hand in coefficients where the frequency of errors was the most "in-between" two expected frequencies given the private key coefficients. This proved tedious, but then we figured out that we have the actual Alice's public key and we could run one final meet-in-the-middle run with this public key and the public key obtained by our private key guess. This would fix the errors in the private key for us, and indeed it did!
hxp{1s0g3n1es__m0rE_L1k3__1_s0_G3n1u5}