Tags: forensics am radio
Rating: 3.0
In this challenge an audio file is given and it is required to find the flag hidden in it.
This is an example of how a challenge should not be solved. For sure there was a better way that we do not know.
By looking at the spectrogram (using sonic visualizer) we can see that there is some sequence hidden at frequency 18k.
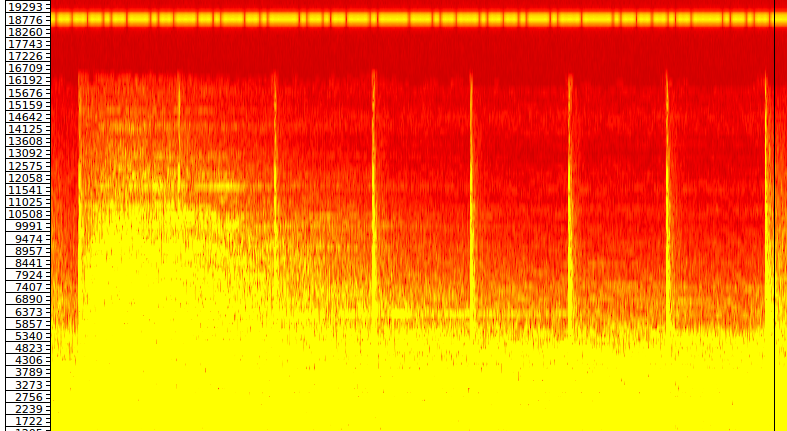
We can use audacity to extract that frequency, by using an high-pass filter and by amplifying the result.
The applied filters are the following
```
- stereo track to mono
- high pass filter (17000, 48 dB)
- amplify (45)
```
We can now see a nice waveform:

Let us export the result and extract the bits contained in this wave. We can use the following lines to extract the bits, by passing a frequency and a threshold.
```
//bits.c
int main(int argc, char *argv[]){
int c,i;
float val = 0;
float alpha = 0.001;
int freq = atoi(argv[1]);
int ts = atoi(argv[2]);
while((c=getchar())!=-1){
c &= 0x0ff;
c = abs(c-128);
val = alpha*c + (1-alpha)*val;
if(i++%freq == freq/2){
printf("%d\n",val<ts?0:1);
}
}
printf("\n");
}
```
By using the following line we can see a sequence of 0 and 1:
```
$ cat filtered.aiff | ./bits 70 40 | tr -d '\n'
...00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000111110000000000000011111100000000000000111111100000000000011111111000000000000011111110000000000000111111100000000000001111111000000000000011111111000000000000111111100000000000000111111100000000000001111111000000000000111111110000000000000111111100000000000001111111100000000000011111111000000000000011111100000000000000111111100000000000011111111000000000000011111110000000000000111111100000000000001111111100000000000011111111000000000000011111110000000000000111111100000000000001111111000000000000011111110000000000000111111100000000000001111111100000000000011111111000000000000011111100000000000000111111111111111111111111111111000000001111111111111111111111111111111110000001111111111111111111111111111111111000000001111111111111111111111111111111100000000111111111111111111111111111111111000000111111111111000000000001111111111111111111111111111111000000001111111111111111111111111111111111111111111111111111100000011111111111100000000000011111111111111111111111111111111111111111111111111111111111111111111111100001111111111111111111111111111111111111111111111111111111100000111111111111000000000001111111111111111111111111111111000000011111111111000000000000111111111111111111111111111111100000000111111111111111111111111111111110000000111111111111111111111111111111111100000001111111111100000000000111111111111111111111111111111100000000...
```
Let us print the length of the 1 sequences:
```
$ cat filtered.aiff | ./bits 70 40 | uniq -c | grep "[0-9] 1" | awk '{print $1}' > data ; cat data
5
6
7
8
7
7
7
8
7
7
7
...
```
Using this command we can see that the lengths are in some way clustered
```
$ cat data | sort -n | uniq
5
6
7
8
10
11
12
13
14
30
31
32
33
34
35
51
52
53
54
55
56
57
71
72
73
74
75
92
93
94
95
112
115
134
154
734
```
Let's print a different number for each cluster:
```
cat data | awk '{if($1<=14)print "0"; else if($1<=35)print "1"; else if ($1<=57)print "2"; else if ($1<=75)print "3"; else if ($1<=95)print "4";else if($1<=115)print "5"; else if($1==134)print "6"; else if($1==154)print "7"}' > data2; cat data2 | tr -d '\n'
000000000000000000000000000000111110120320101110120121021030101203201201102023011101301012011102010122011101201210230120220220131010210401020250110210401401102103040104030212012012101201310130104110520102110313010410220120122011230213030301602104012202220301110114012021040150302120130704022101120202406020140110111023032013201201210201320203120220210401210112110
```
Let's now consider 0 to be a separator:
```
$ cat data2 | tr -d '\n' | tr '0' ' '
11111 12 32 1 111 12 121 21 3 1 12 32 12 11 2 23 111 13 1 12 111 2 1 122 111 12 121 23 12 22 22 131 1 21 4 1 2 25 11 21 4 14 11 21 3 4 1 4 3 212 12 121 12 131 13 1 411 52 1 211 313 1 41 22 12 122 1123 213 3 3 16 21 4 122 222 3 111 114 12 21 4 15 3 212 13 7 4 221 112 2 24 6 2 14 11 111 23 32 132 12 121 2 132 2 312 22 21 4 121 11211
```
By looking at the frequencies of the various subsequences we can see that it could be some alphabet:
```
$ cat data2 | tr -d '\n' | tr '0' ' ' | tr ' ' '\n' | sort | uniq -c | sort -nr
30
12 12
10 1
8 4
7 3
7 21
7 2
6 111
5 121
4 22
4 11
3 32
3 23
3 13
3 122
2 212
2 14
2 132
2 131
1 7
1 6
1 52
1 411
1 41
1 313
1 312
1 25
1 24
1 222
1 221
1 213
1 211
1 16
1 15
1 114
1 1123
1 11211
1 112
1 11111
```
Let's suppose that 1 represents a space:
```
$ cat data2 | tr -d '\n' | tr '0' ' ' | sed 's/ 1 / /g'
11111 12 32 111 12 121 21 3 12 32 12 11 2 23 111 13 12 111 2 122 111 12 121 23 12 22 22 131 21 4 2 25 11 21 4 14 11 21 3 4 4 3 212 12 121 12 131 13 411 52 211 313 41 22 12 122 1123 213 3 3 16 21 4 122 222 3 111 114 12 21 4 15 3 212 13 7 4 221 112 2 24 6 2 14 11 111 23 32 132 12 121 2 132 2 312 22 21 4 121 11211
```
We can see that there are some space in the first part, and no spaces on the second part. Thus, the second part could be the flag.
By replacing 41, 22, 12, 122, with f,l,a,g and then continuing to guess other characters considering their frequencies, we can find the meaning of each subsequence.
The substitutions are the following (we still don't know if this is some existing encoding):
```
41 f
22 l
12 a
122 g
111 r
2 e
121 d
21 i
3 o
32 m
11 t
23 u
13 s
22 l
131 y
4 n
25 x
14 c
212 w
24 S
6 p
1123 {
11211 }
132 M
312 B
3 o
16 k
222 F
114 R
213 L
15 b
7 I
221 T
112 h
```
The flag is
```
flag{LookingForRainbowsInTheSpectrumMadeMeBlind}
```