# The worst RSA Joke

Here's the challenge:

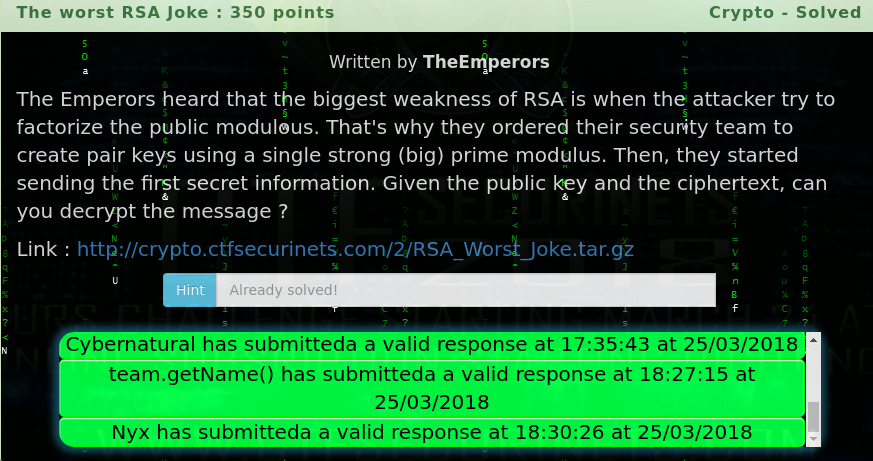
Here's is the given tar.gz
[RSA_Worst_Joke.tar.gz](https://github.com/ozancetin/CTF-Writeups/blob/master/2018/Securinets%20CTF%20Quals%202018/The%20worst%20RSA%20Joke/RSA_Worst_Joke.tar.gz?raw=true)

Include encrypted flag and public key
[flag.enc](https://github.com/ozancetin/CTF-Writeups/raw/master/2018/Securinets%20CTF%20Quals%202018/The%20worst%20RSA%20Joke/flag.enc) and [public.pem](https://github.com/ozancetin/CTF-Writeups/raw/master/2018/Securinets%20CTF%20Quals%202018/The%20worst%20RSA%20Joke/public.pem)

First of all you need to understand, How does RSA work?

One of the reasons RSA is so popular is the simplicity of the cryptosystem. Here are the basic steps of RSA Encryption and Decryption.

1) Choose two (usually large) primes, p and q
2) Compute a value N = p*q, commonly reffered to as the modulus
3) Compute φ(N) = (p-1)*(q-1)
4) Choose a "public exponent value", denoted e. Typically this is 3 or 65537.
5) Compute d, the "private exponent value" which is the multiplicitve inverse of e mod(φ(N))
6) To encrypt a message m, compute m^e mod (N)
7) To decrypt a ciphertext c, compute c^d mod (N)

But we got a problem in there normally we must have 2 prime numbers but question said to us "their security team to create pairs key using A SINGLE STRONG(BIG) PRIME MODULUS. Which means that, there are no 2 prime numbers there is a only p. So I research in google about single prime modulus rsa and found some article:


source: https://math.stackexchange.com/questions/1077411/textbook-rsa-game-with-one-prime

So in this article we dont need to any factorization we already have p, N, e, c. We just need to find d that formula
```
N = 36511974694593690272644354864534934200522045623187752384823594729275730789191680514905027084950729514148679507005058047146031869995768765034876499069680202424692876360895377987654388335335689563844006584610187090074654410815638237841872991488680663410743679302763304922852173164820002226109196761249018548478251723505481964749218302723593776180246783117481280725673997940309717028451914887375722437833384305529884261542397905220138488012276363046571670926597766521674838665982314321651508118240682649024780239598188845543243957916954287138820155843952556411235376764737602711594439293285811102883736229645274092478611

e = 65537

for in this challege N = p

φ(p) = p−1

φ(p) = 36511974694593690272644354864534934200522045623187752384823594729275730789191680514905027084950729514148679507005058047146031869995768765034876499069680202424692876360895377987654388335335689563844006584610187090074654410815638237841872991488680663410743679302763304922852173164820002226109196761249018548478251723505481964749218302723593776180246783117481280725673997940309717028451914887375722437833384305529884261542397905220138488012276363046571670926597766521674838665982314321651508118240682649024780239598188845543243957916954287138820155843952556411235376764737602711594439293285811102883736229645274092478610

c = 1237246926259160194461212150945844715199415065489186503438046391250572086566421899895065862617481835552501670206131393989349579699016250645381272784853486298867487101312029656557709181513285660622551038697097104516040415941833312707266663073808342388097795983423218921449288935929266341870231606976459956241911038410679913543232013864543934267311164641603092384739030006128391776282830565811471399620276910709109729529350609477615417839951168576668481073856643110426251453372087077248671240669626996120729874993428891060062802375925819679475655055992800126080905876517050068726446140528616284985948190890833343865076
```
So let me show you, How to find these values:

Finding N and e with openssl


Finding c

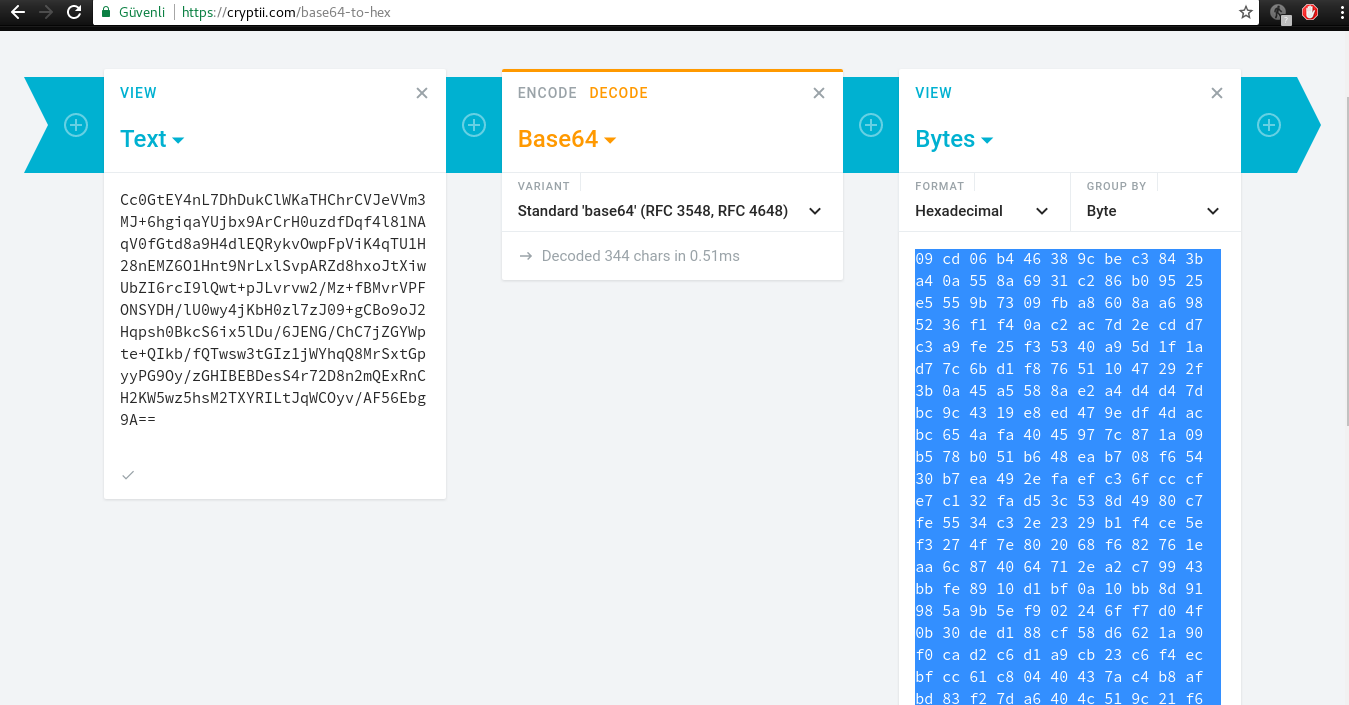
I dont know I couldnt convert base64 to hex. some lib issue so I quickly try online tool

As you can see we already have c,e,N,p,φ(p) now we will find d:
that formula

de ≡ 1 mod φ(p)

we need to do modular multiplicative inverse, using gmpy lib in python

using: gmpy.invert(e, φ(p))
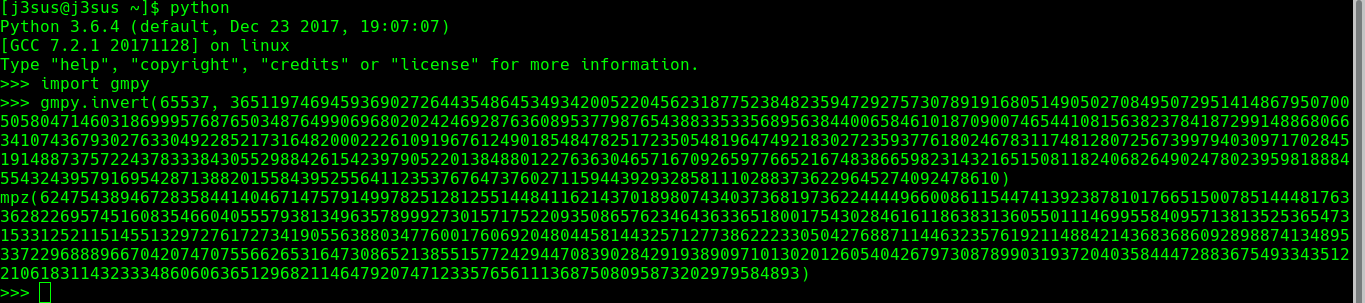
```d = 6247543894672835844140467147579149978251281255144841162143701898074340373681973622444496600861154474139238781017665150078514448176336282269574516083546604055579381349635789992730157175220935086576234643633651800175430284616118638313605501114699558409571381352536547315331252115145513297276172734190556388034776001760692048044581443257127738622233050427688711446323576192114884214368368609289887413489533722968889667042074707556626531647308652138551577242944708390284291938909710130201260540426797308789903193720403584447288367549334351221061831143233348606063651296821146479207471233576561113687508095873202979584893```

So now we can finish this job with pow(c,d,N)

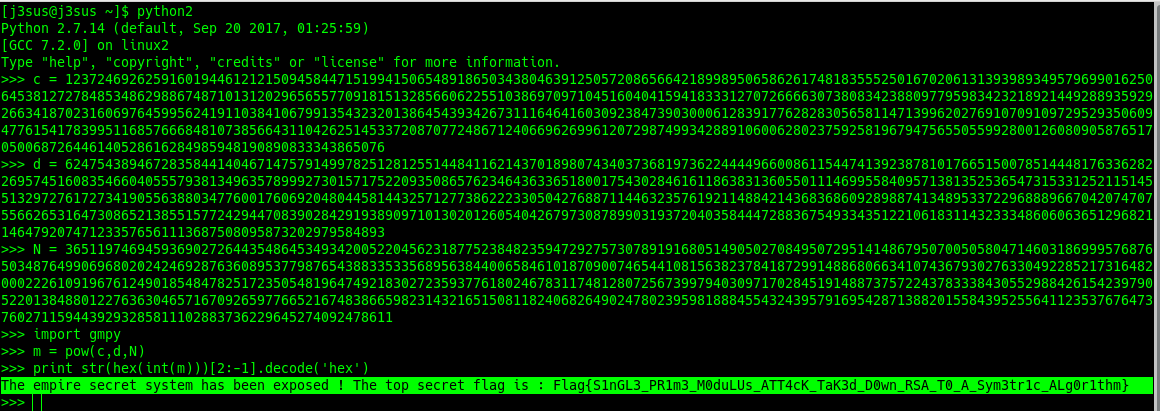
Finally here's the plaintext and flag:
```
The empire secret system has been exposed ! The top secret flag is : Flag{S1nGL3_PR1m3_M0duLUs_ATT4cK_TaK3d_D0wn_RSA_T0_A_Sym3tr1c_ALg0r1thm}
```

Original writeup (https://github.com/ozancetin/CTF-Writeups/blob/master/2018/Securinets%20CTF%20Quals%202018/The%20worst%20RSA%20Joke/README.md).