# It's Not My Fault 2
(https://github.com/Ethan127/CTF_writeups/edit/main/picoCTF_2021/Cryptography/it's-not-my-fault-2/)

**PROBLEM**

We need to find p + q, and we know the public modulus, n, and the public exponent, e (which the problem calls "clue"). We also know that e was generated using the two Chinese Remainder Theorem exponents, dp and dq. Lastly, we know that dp is at most 36 bits.

n = 124820867833961512255121751609049306179897666404096891662718071264088624606195417583639161066276975279640599118437354335640828498035985542095139168119692839404116968042389114810846687132156292424607681366934277727898599922856113752913454673986423798381847193428071452354375463030105066256138253881897882994099
e = 46413346084333645012143147319389347924397373027897998120051654242937480130282545034433967290231436105403203157816717530203079607233722565425714290923944628662988841561125900662835135189696637301075373141006198752365262569240099036001408525284187514463343741272674488593785654318061637768053550355072803501569

**HINTS**

None.

**SOLUTION**

Firstly, this problem requires finding a particular MD5 hash as a PoW (proof of work). I provided a simple script to do that.

The solution for It's Not My Fault 1 would not work here. It would likely run for a completely infeasible length of time.

The solution can be found on page 529 of *Mathematics of Public Key Cryptography* by Steven D. Galbraith. The solution is also described on [MathOverflow](https://mathoverflow.net/questions/120160/attack-on-crt-rsa).

In essence, for any random number m, there is a high probability that  has a greatest common denominator with n of p, evaluated at one point with input . L is the square root of the maximum possible value for dp and l is an integer 0 < l < L.

In this case, L=2^18 (square root of 2^36), so we have to evaluate gcd(G(x), n) at 2^18 different values of l. To this, it is useful to use the method of fast multipoint evaluation found in *Modern Computer Algebra: 3rd Edition* beginning on page 295. Alternatively, more information and a proof can be found [here](http://www.cecm.sfu.ca/CAG/theses/justine.pdf).

Luckily, sagemath has excellent support for polynomial arithmetic. To construct the polynomial, sagemath has the useful prod function, which multiplies polynomials in a list.
```python
def interpolate(n, e, L, m):
FR.<x> = PolynomialRing( IntegerModRing(n) )
f = prod([(m.powermod(e*l-1, n)*x - 1) for l in range(1,L)])
print("Done building poly.")
return f
```

PolynomialRing takes a ring as input. In this case, the ring is 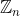, because everything is modulo n.

To evaluate the polynomial at so many points, it is useful to build a subproduct tree (explained in greater depth in *Modern Computer Algebra: 3rd Edition*) and then recursively divide down it until the remainder is a polynomial of degree 0 (just an integer). Each time downTree is called, it computes the remainder whan the polynomial is the divided by the left branch and the right branch of the subproduct tree, stored as r0 and r1, respectively. It then is recursively called with (r0, left branch) and (r1, right branch) as the new polynomial and subproduct tree until the remainder is just an integer. This integer is one evaluation of G(x) at a particular value of x. After the recursion terminates, downTree will return a list, in order, of G(x0), G(x1), etc.
```python
def constructTree(nodes, mo):
FR.<x> = PolynomialRing( IntegerModRing(mo) )
if len(nodes)==2:
return Node("Subproduct Tree", nodes[0], nodes[1])
newnodes = []
for i in range(len(nodes)-1):
if i%2==0:
newnodes.append(Node( nodes[i].data*nodes[i+1].data, nodes[i], nodes[i+1] ))
return constructTree(newnodes, mo)

def subproductTree(points, mo):
FR.<x> = PolynomialRing( IntegerModRing(mo) )
print("Building subproduct tree...")
base = []
start = time.time()
for j in range(len(points)):
base.append(Node(x-points[j]))
end = time.time()
print("Done building base of subproduct tree. Took "+str((end-start)/60)+" minutes.")
start = time.time()
tree = constructTree(base, mo)
end = time.time()
print("Done building subproduct tree. Took "+str((end-start)/60)+" minutes.")
return tree

def downTree(f, tree, mo):
FR.<x> = PolynomialRing( IntegerModRing(mo) )
if len(f.coefficients())==1:
return f.coefficients()
start = time.time()
r0 = f.quo_rem(tree.left.data)[1]
r1 = f.quo_rem(tree.right.data)[1]
end = time.time()
if len(f.coefficients())==1:
return f.coefficients()
return downTree(r0, tree.left, mo) + downTree(r1, tree.right, mo)
```

Also, since the subproduct tree is a binary tree, I created a basic binary tree class as a data structure.
```python
class Node: #binary tree
def __init__(self, data, left=None, right=None):
self.left = left
self.right = right
self.data = data
```
After the function returns the list of evaluations, all that is needed to do is to check, one at a time, if the greatest common denominator with n is greater than 1. If it is, the gcd is p. q can be found by dividing n by p.

Putting this all together, the script runs for a little over 3 minutes and produces the follow output:
```
N = 124820867833961512255121751609049306179897666404096891662718071264088624606195417583639161066276975279640599118437354335640828498035985542095139168119692839404116968042389114810846687132156292424607681366934277727898599922856113752913454673986423798381847193428071452354375463030105066256138253881897882994099
E = 46413346084333645012143147319389347924397373027897998120051654242937480130282545034433967290231436105403203157816717530203079607233722565425714290923944628662988841561125900662835135189696637301075373141006198752365262569240099036001408525284187514463343741272674488593785654318061637768053550355072803501569
P = 10981294651751279806515108287557638517630455343550832378206374863939727133228243364462266288660844847965994404052324588619140511298150066664108753959728951
Q = 11366680504657551850701503649895132354141527614114028624146263675620249881060523500841798021203665778501194590257517985266001557737176910239108735881800549
D = 39703685433221688073441805738106937370231071075917136648921224037977345322990581624974903406178920243086789523154987533535736292881197119940200695278446983814185461024786053606276217414890014701018698542474032686858900876398670775449792115942224720966744268282577390483150534252773589178384971494662329284929
Dp = 23719671579
Dq = 10004692956684517761402598130455900330030145484915696435010222273980676870337086650825782158410036730561416392714266700633551827509694417218689441967159525
P + Q = 22347975156408831657216611937452770871771982957664861002352638539559977014288766865304064309864510626467188994309842573885142069035326976903217489841529500
```

FLAG - picoCTF{p0lyn0m14l_4r17hm371c_73chn1qu35_4r3_u53ful_1n_m4ny_f13ld5!!!}

Original writeup (https://github.com/Ethan127/CTF_writeups/edit/main/picoCTF_2021/Cryptography/it's-not-my-fault-2/).