# Hidden Key
Cryptography - 250 points

## Challenge

> Ugh, another RSA problem? Help me decrypt this [message](Hidden_Key.txt) please.

## Solution

### RSA







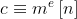
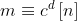
### Script

```
n=23771394852910639082583501669530890953667541327452385339244879173587989064734577446471102994475189372684743795254735451944597143864549235990591729400340618643634331527928443630441118443293131567768102415899778261766094189544469362494173326242393482896618565916197135201551162898936577373806915526433247080527802988058032843358388910692815849911082186689778983514879268314194473412440350826066014379363598141942960876294951059670494304420783931550196576699781466293767367193560268678763964125161618511034351111453843215077891836707748402326693186380606250308456070456770861623489696650199318523543231853596082763712307
e=65537
c=15152801953478615231615813174158717826208918111757011747988906836426502895099242747835026205340656958975116313161051866115947302881237114983857653344685927368449097875645938338991888932698175908609811160840398889905427433799960012502893930361988001955295067071781029506130517204169795490975096203536618808080762347655332301145660198939248232962193390588038274758393252137503862620577494319064425602342789523724094298326178304046723002691324112726623878745995975972547721658598172533473268445493568838058261665674787313810379877275689561385909748399944470056206680588572965450454425734736206241548497125876627033884987
# twodphi = 2d+phi(n)
twodphi=37522002584021955249340303907837741680028779890763490946928681750311376852458883273648415268771456048279882988048226472028209114566672640119607895254238612948838681867793974521846321613795940938567631881495710237650749128367284467429616065425589798513915815315514061449179290300231809811071669293115951458555128955662862598401276723507543847080962220156185664629981885527698794059633761338150274671561342202316529169921166193284138591003891171560545510890577376532942003959005722155615213049952143695803658907536762317179556353262346224586373466082695017756636007707783853318052447290904520185444458711097071045593826

def breakIt(n,e,twodphi):
mtest = 42
ctest = pow(mtest, e, n)

for k in range(100001,999999, 2):
k=103447
phi = (e*twodphi - 2) // k
d = (twodphi - phi) >> 1 # k >> 1 <=> k * 1/2
if d > 0:
if pow(ctest, d, n) == mtest:
print "d : ",d
print
m = pow(c, d, n)
print(hex(m)[2:].rstrip('L').decode('hex'))
return

breakIt(n,e,twodphi)
```

Flag :
```
easyctf{4rfyb2ud5eixw5dssu}
```